We’re back at it in the Proof of Work difficulty spectrum, this time going through how Ethereum’s difficulty changes over time. This is part 4.2 of the part 4 series, where part 4.1 was about Bitcoin’s PoW difficulty, and the following 4.3 will be about jbc’s PoW difficulty.
TL;DR
To calculate the difficulty for the next Ethereum block, you calculate the time it took to mine the previous block, and if that time difference was greater than the goal time, then the difficulty goes down to make mining the next block quicker. If it was less than the time goal, then difficulty goes up to attempt to mine the next block quicker.
There are three parts to determining the new difficulty: offset, which determines the standard amount of change from one difficulty to the next; sign, which determines if the difficulty should go up or down; and bomb, which adds on extra difficulty depending on the block’s number.
These numbers are calculated slightly differently for the different forks, Frontier, Homestead, and Metropolis, but the overall formula for calculating the next difficulty is
target = parent.difficulty + (offset * sign) + bomb
Other Posts in This Series
- Part 1 — Creating, Storing, Syncing, Displaying, Mining, and Proving Work
- Part 2 — Syncing Chains From Different Nodes
- Part 3 — Nodes that Mine
- Part 4.1 — Bitcoin Proof of Work Difficulty Explained
Pre notes
For the following code examples, this will be the class of the block.
class Block():
def __init__(self, number, timestamp, difficulty, uncles=None):
self.number = number
self.timestamp = timestamp
self.difficulty = difficulty
self.uncles = uncles
The data I use to show the code is correct was grabbed from Etherscan.
The code doesn’t include edge cases in calculating the difficulty either. For the most part, edge cases aren’t involved in calculating the difficulty target. By not including them, it makes the following code much easier to understand. I’ll talk about the edge cases at the end to make sure they’re not completely ignored.
Finally, for the beginning fork, I talk about what the different variables and functions perform. For later forks, Homestead and Metropolis, I only talk about the changes.
Also, here’s all the code I threw in a Github repo! If you don’t want to write all the code yourself, you should at least clone it locally and run it yourself. 1000% feel free to make pull requests if you want to add more parts to it or think I formatted the code wrong.
The Beginning — Frontier
In the beginning, there was Frontier. I’ll jump right in by giving a bullet point section going over the config variables.
DIFF_ADJUSTMENT_CUTOFF— Represents the seconds that Ethereum is aiming to mine a block at.BLOCK_DIFF_FACTOR— Helps calculate how much the current difficulty can change.EXPDIFF_PERIOD— Denotes after how many blocks the bomb amount is updated.EXPDIFF_FREE_PERIODS— How manyEXPDIFF_PERIODSare ignored before including the bomb in difficulty calculation.
And now descriptions of the functions.
calc_frontier_sign — Calculates whether the next difficulty value should go up or down. In the case of Frontier, if the previous block was mined quicker than the 13 seconds DIFF_ADJUSTMENT_CUTOFF, then the sign will be 1, meaning we want the difficulty to be higher to make it more difficult with the goal that the next block be mined more slow. If the previous block was mined longer than 13 seconds, then the sign will be -1 and the next difficulty will be lower. The overall point of this is that the goal for block mining time is ~12.5 seconds. Take a look at Vitalik Buterin’s post where he talks about choosing 12 seconds at the minimum average block mining time.
calc_frontier_offset — Offset is the value that determines how much or how little the difficulty will change. In the Frontier, this is the parent’s difficulty integer devided by the BLOCK_DIFF_FACTOR. Since it’s devided by 2048, which is 2^11, offset can also be calculated by parent_difficulty >> 11 if you want to look at it in terms of shifting bits. Since 1.0 / 2048 == 0.00048828125, it means that the offset will only change the difficulty by 0.0488% per change. Not that much, which is good because we don’t want the difficulty to change a ton with each different mined block. But if the time becomes consistently under the 13 seconds cutoff, the difficulty will slowly grow to compensate.
calc_frontier_bomb — The bomb. The bomb adds an amount of difficulty that doubles after every EXPDIFF_PERIOD block is mined. In the Frontier world, this value is incredibly small. For example, at block 1500000, the bomb is 2 ** ((1500000 // 100000) - 2) == 2 ** 15 == 32768. The difficulty of the block is 34982465665323. That’s a huge difference meaning that the bomb took on zero affect. This will change later.
calc_frontier_difficulty — Once you have the values for sign, offset, and bomb, the new difficulty is (parent.difficulty + offset * sign) + bomb. Let’s say that the the time it took to mine the parent’s block was 15 seconds. In this case, the difficulty will go down by offset * -1, and then add the small amount of the bomb at the end. If the time to mine the parent’s block was 8 seconds, the difficulty will increase by offset + bomb.
In order to understand it fully, go through the code that follows and look at the calculations.
config = dict(
DIFF_ADJUSTMENT_CUTOFF=13,
BLOCK_DIFF_FACTOR=2048,
EXPDIFF_PERIOD=100000,
EXPDIFF_FREE_PERIODS=2,
)
def calc_frontier_offset(parent_difficulty):
offset = parent_difficulty // config['BLOCK_DIFF_FACTOR']
return offset
def calc_frontier_sign(parent_timestamp, child_timestamp):
time_diff = child_timestamp - parent_timestamp
if time_diff < config['DIFF_ADJUSTMENT_CUTOFF']:
sign = 1
else:
sign = -1
return sign
def calc_frontier_bomb(parent_number):
period_count = (parent.number + 1) // config['EXPDIFF_PERIOD']
period_count -= config['EXPDIFF_FREE_PERIODS']
bomb = 2**(period_count)
return bomb
def calc_frontier_difficulty(parent, child_timestamp):
offset = calc_frontier_offset(parent.difficulty)
sign = calc_frontier_sign(parent.timestamp, child_timestamp)
bomb = calc_frontier_bomb(parent.number)
target = (parent.difficulty + offset * sign) + bomb
return offset, sign, bomb, target
The Middle — Homestead
The Homestead fork, which took place at block number 1150000 in March of 2016, has a couple big changes with calculating the sign.
calc_homestead_sign — Instead of having a single number, DIFF_ADJUSTMENT_CUTOFF which is different for the Homestead fork, that makes the difficulty go up or down, Homestead takes a slightly different approach. If you look at the code, you’ll see that that there are groupings of the sign rather than either 1 or -1. If the time_diff between grandparent and parent is in [0,9], sign will be 1, meaning that difficulty needs to increase. If the time_diff is [10,19], the sign will be 0 meaning that the difficulty should stay as it is. If the time_diff is in the range [20, 29], then the sign becomes -1. If time_diff is in the range [30,39], then the sign is -2, etc.
This does two things. First, Homestead doesn’t want to equate a block that took 50 seconds to mine as being the same as a block that took 15 seconds to mine. If it took a block 50 seconds, then the next difficulty in fact does need to be easier. Secondly, instead of DIFF_ADJUSTMENT_CUTOFF representing the goal time, this switches the aim point to be the mid point of the range of time_diffs with a sign of 0. [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]. Meaning ~14.5 seconds, not including the bomb.
config = dict( HOMESTEAD_DIFF_ADJUSTMENT_CUTOFF=10, BLOCK_DIFF_FACTOR=2048, EXPDIFF_PERIOD=100000, EXPDIFF_FREE_PERIODS=2, ) def calc_homestead_offset(parent_difficulty): offset = parent_difficulty // config['BLOCK_DIFF_FACTOR'] return offset def calc_homestead_sign(parent_timestamp, child_timestamp): time_diff = child_timestamp - parent_timestamp sign = 1 - (time_diff // config['HOMESTEAD_DIFF_ADJUSTMENT_CUTOFF']) return sign def calc_homestead_bomb(parent_number): period_count = (parent_number + 1) // config['EXPDIFF_PERIOD'] # or parent.number + 1 >> 11 if you like bit notation period_count -= config['EXPDIFF_FREE_PERIODS'] bomb = 2**(period_count) return bomb def calc_homestead_difficulty(parent, child_timestamp): offset = calc_homestead_offset(parent.difficulty) sign = calc_homestead_sign(parent.timestamp, child_timestamp) bomb = calc_homestead_bomb(parent.number) target = (parent.difficulty + offset * sign) + bomb return offset, sign, bomb, target
The Current — Metropolis
There are a couple differences from Homestead. First is that the DIFF_ADJUSTMENT_CUTOFF is now 9, which means that, without uncles, the target block time is midpoint of [9, 10, 11, 12, 13, 14, 15, 16, 17] or ~13 seconds.
The second takes into account whether or not there are uncles included in the block. And uncle in Ethereum language refers to a point in time where two nodes mine a child block from the same grandparent. So if you’re mining a child block from a parent that has a “sibling”, you’re able to pick one of the siblings to mine from, but also include that you noticed the other block. In that case, Ethereum wants to make the new difficulty larger, buy another offset, to make sure that there is a less likely chance for two natural forks to get much longer.
Now the biggest difference is dissolving the impact of the bombs. Check out the code for calc_metropolis_bomb where not only do we subtract the value of EXPDIFF_FREE_PERIODS, but also METROPOLIS_DELAY_PERIODS which is 30 time periods. A huge number. Instead of talking about the bombs here, I’ll have a section devoted to that after this.
config = dict(
METROPOLIS_DIFF_ADJUSTMENT_CUTOFF=9,
BLOCK_DIFF_FACTOR=2048,
EXPDIFF_PERIOD=100000,
EXPDIFF_FREE_PERIODS=2,
METROPOLIS_DELAY_PERIODS=30,
)
def calc_metropolis_offset(parent_difficulty):
offset = parent_difficulty // config['BLOCK_DIFF_FACTOR']
return offset
def calc_metropolis_sign(parent_timestamp, child_timestamp):
if parent.uncles:
uncles = 2
else:
uncles = 1
time_diff = child_timestamp - parent_timestamp
sign = uncles - (time_diff // config['METROPOLIS_DIFF_ADJUSTMENT_CUTOFF'])
return sign
def calc_metropolis_bomb(parent_number):
period_count = (parent_number + 1) // config['EXPDIFF_PERIOD']
period_count -= config['METROPOLIS_DELAY_PERIODS'] #chop off 30, meaning go back 3M blocks in time
period_count -= config['EXPDIFF_FREE_PERIODS'] #chop off 2 more for good measure
bomb = 2**(period_count)
return bomb
def calc_metropolis_difficulty(parent, child_timestamp):
offset = calc_metropolis_offset(parent.difficulty)
sign = calc_metropolis_sign(parent_timestamp, child_timestamp)
bomb = calc_metropolis_bomb(parent.number)
target = (parent.difficulty + offset * sign) + bomb
return offset, sign, bomb, target
Going Deeper with the Bombs
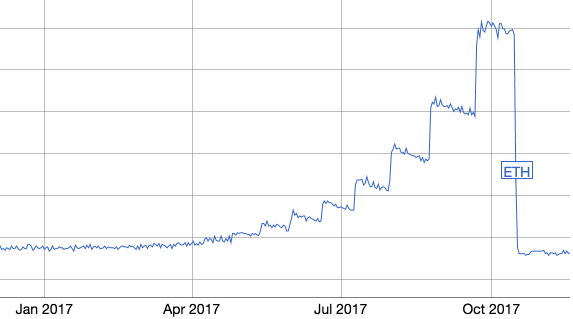
If you look at one of the difficulty charts from online, you’ll see a recent amount of huge increasing jumps every 100000 blocks, and then a giant drop off about a month ago. Screenshot time for those not wanting to click the link:
What’s the point of having a bomb like this? A big goal of Ethereum is to get rid of Proof of Work, which requires energy and time to create and validate a new block, into Proof of Stake, which is described in the Ethereum Wiki. In order to force nodes to move to the Proof of Stake implementation, a “bomb” that doubles its impact on the difficulty every 100000 blocks would soon make it take so long to mine a new block, the nodes running on the old fork won’t be able to run anymore. This is where the term “Ice Age” comes from; the block chain would be frozen in time.
This is a good way to manage future changes, but also we run into the issue that the new Proof of Stake implementation, called Casper, wasn’t ready in time before the giant difficulty spikes seen in that graph. That’s where the Metropolis fork came into play — it eliminated the effect the bomb has on the difficulty, but in a few years it will come back into play, where the switch to Casper will (hopefully) be ready to roll. That being said, predicting when features like this fork are ready for production and adoption is difficult, so if Casper isn’t ready to be pushed quick enough, you can create another fork that moves the bomb back in time again.
Bomb Math
Besides the description of what the bombs do to the difficulty as seen on those graphs, it’s worth it to show the math behind why the difficulty is rising to those levels, and what that means for how long it takes to mine a block.
Going back, remember that offset is an indicator of how much it takes a node to mine a block.
For example, if the previous time difference between blocks was [18-26], we say that if we decrease difficulty by an offset, we’ll be able to move the time to mine a block back to the [9-17] range, or DIFF_ADJUSTMENT_CUTOFF seconds lower.
So if we increase the difficulty by offset, we expect the time it takes to mine a block to increase by DIFF_ADJUSTMENT_CUTOFF. If we increase the difficulty by half of an offset, the mining time should increase by about DIFF_ADJUSTMENT_CUTOFF / 2.
So if we want to see how much a bomb will influence the change in mining time, we want the ratio of bomb and offset.
(bomb / offset) * DIFF_ADJUSTMENT_CUTOFF
Here’s the code that shows how we can calculate the time it takes to mine and compare to the actual average time, where actual average mining time was gathered from this chart by hovering the cursor around where in time these blocks were mined.
def calc_mining_time(block_number, difficulty, actual_average_mining_time, calc_bomb, calc_offset): homestead_goal_mining_time = 14.5 #about that. bomb = calc_bomb(block_number) offset = calc_offset(difficulty) bomb_offset_ratio = bomb / float(offset) seconds_adjustment = bomb_offset_ratio * config['HOMESTEAD_DIFF_ADJUSTMENT_CUTOFF'] average_mining_time = 0.4 * 60 calculated_average_mining_time = homestead_goal_mining_time + seconds_adjustment print "Bomb: %s" % bomb print "Offset: %s" % offset print "Bomb Offset Ratio: %s" % bomb_offset_ratio print "Seconds Adjustment: %s" % seconds_adjustment print "Actual Avg Mining Time: %s" % actual_average_mining_time print "Calculated Mining Time: %s" % calculated_average_mining_time print block_number = 4150000 difficulty = 1711391947807191 actual_average_mining_time = 0.35 * 60 calc_mining_time(block_number, difficulty, actual_average_mining_time, calc_homestead_bomb, calc_homestead_offset) block_number = 4250000 difficulty = 2297313428231280 actual_average_mining_time = 0.4 * 60 calc_mining_time(block_number, difficulty, actual_average_mining_time, calc_homestead_bomb, calc_homestead_offset) block_number = 4350000 difficulty = 2885956744389112 actual_average_mining_time = 0.5 * 60 calc_mining_time(block_number, difficulty, actual_average_mining_time, calc_homestead_bomb, calc_homestead_offset) block_number = 4546050 difficulty = 1436507601685486 actual_average_mining_time = 0.23 * 60 calc_mining_time(block_number, difficulty, actual_average_mining_time, calc_metropolis_bomb, calc_metropolis_offset)
When run:
Bomb: 549755813888 Offset: 835640599515 Bomb Offset Ratio: 0.657885476372 Seconds Adjustment: 6.57885476372 Actual Avg Mining Time: 21.0 Calculated Mining Time: 21.0788547637 Bomb: 1099511627776 Offset: 1121735072378 Bomb Offset Ratio: 0.980188330427 Seconds Adjustment: 9.80188330427 Actual Avg Mining Time: 24.0 Calculated Mining Time: 24.3018833043 Bomb: 2199023255552 Offset: 1409158566596 Bomb Offset Ratio: 1.56052222062 Seconds Adjustment: 15.6052222062 Actual Avg Mining Time: 30.0 Calculated Mining Time: 30.1052222062 Bomb: 8192 Offset: 701419727385 Bomb Offset Ratio: 1.16791696614e-08 Seconds Adjustment: 1.16791696614e-07 Actual Avg Mining Time: 13.8 Calculated Mining Time: 14.5000001168
Look how large the bomb offset ratio is for the later Homestead blocks, and how tiny it becomes after the Metropolis block! With the loss of the bomb’s impact, the time difference drops a crap ton.
As of now, the bomb doesn’t affect the difficulty by pretty much any amount. It’ll be back though. If Ethereum continues to mine blocks at the rate of ~14.5 seconds, they’ll have 100,000 mine blocks in around 17 days. Multiply that time by 30, which accounts for the METROPOLIS_DELAY_PERIODS, we’ll be back in a state where the bomb makes a difference in around a year and a half, no matter how much the hash power increases.
Bomb Equilibrium
The last part of bomb dealing is to quickly explain why a slight increase in the bomb will make the overall difficulty be raised to a much higher value compared to how large the bomb value is.
The thought on how this works is by taking the calculated expecting mining time and from there calculating the difficulty required by the current hash rate to mine blocks in that time period. When the bomb amount changes, the difficulty will continue to rise or fall to get to the difficulty for that time, and then hover in that equilibrium. If you look at the blocks right after the bomb change, you’ll see it takes more than a few blocks to get to the new level.
The Edge Cases
There are a couple edge cases here not mentioned in the code above.
- MIN_DIFF=131072, which is the minimum difficulty a block can have. Considering the difficulty is incredibly larger than that, it’s pointless to think about that. But when Ethereum was gerenerated, it was probably useful to have a minimum difficulty. Also can be refered to as 2 ** 17.
- Smallest sign = -99. Imagine a situation where, for some reason, the sign for calculating the next block is -1000. The sign for the next block’s difficulty will drop by an incredible amount which would mean it’d take something like 1000 blocks to get back to the desired ~14 second mining time since the largest difficulty increasing sign is 1 (or two if it includes an uncle). Odds are very very very unlikely that any thing lower than -99 would happen, but still needs to covered.
Final Questions
Like before, here’s a list of questions I had when writing this that didn’t get put in the main post.
What’s in the header?
I’m sure this question will come up a lot when only talking about Proof of Work difficulty. It’s great that we know how difficulty is calculated, but how to validate a block has a valid header is beyond this post.
I’m not going to explain it here, but probably in a future post when I decide how jbc’s header should be calculated after I implement transactions.
I will note that Bitcoin’s header is incredibly simple where the values are smashed together (making sure that the way the bits are combined have the right endian). Ethereum’s is much more complicated by dealing with transactions using a cash method rather than a Merkel tree.
How do you go through and figure this out?
There are tons of posts out there like this one, but frankly, most are very high level with either descriptions, numbers, but not many showing code that calculates those numbers. My goal is to do all of those.
That means that to get to complete understanding to talk about them all, I go through and look at the code bases. Here’s the calc_difficulty function from the Python repo, calcDifficulty from c++, and calcDifficulty from Go. Another bigger point that I keep talking about is that looking at the code doesn’t do much at all, what you need to do is implement similar code yourself.
All of those time estimations include a ~ before a number. Why is that necessary?
That’s a really good question. And the main answer is uncertainty in how many nodes are trying to mine blocks, as well as randomness. If you look at the difficulty chart and zoom in to a timespan of a couple days, you’ll see how random it gets. It’s the same with the average mining time for a specific day. They fluctuate, and so we can’t say exactly what time we expect.
Proof of Work is all I hear people talk about, but it isn’t universal, right?
Correct! I mentioned it above, and I’m betting that if you’re reading this much about Ethereum and you’re all the way at the bottom of this post that you’ve heard of the term Proof of Stake. This is the new option that a major cryptocurrency blockchain hasn’t implemented yet. There are other types of block validation out there. The big upcoming Enterprise versions of blockchains probably won’t be completely based in Proof of Work at all.
The biggest indicator of what type of validation blockchains will use depends on the use cases. Cryptocurrencies need something completely un-fraudable. Same with a blockchain that might store information on who owns what piece of land. We don’t want people to be able to change ownership. But a blockchain that’s used to store something less insanely valuable doesn’t need to waste all that energy. I know some of these other Proofs of validity will come into play in the next few years.
You wrote something confusing / didn’t explain it well enough. What should I do?
Get in freaking contact. Seriously, tons of posts out there that talk about results but don’t say how they calculated it and assume that everyone is as smart as them and know what’s going on. I’m trying to be the opposite where I don’t say something without fully explaining. So if there’s something confusing or wrong, contact me and I’ll make sure to fix the issue.
Can I DM you on Twitter?
Do you like cats or dogs better?
Cats.